Структура данных 2-3-4 дерево. 2-3-4 дерева введение

Структура данных 2-3-4 дерево. 2-3-4 дерева введение

Каждый узел дерева 2-3-4 имеет максимум четыре байтовых точки и три элемента данных. Числовое значение 2, 3 и 4 в имени относится к числу дочерних узлов, которые может содержать узел. Существует три возможных сценария для неконечных узлов:

① узел с элементом данных всегда имеет два дочерних узла;

② узел с двумя элементами данных всегда имеет три дочерних узла;

③ узел с тремя элементами данных всегда имеет четыре дочерних узла;

Короче говоря, число дочерних узлов неконечного узла всегда на 1 больше, чем элементов данных, которые он содержит. Если количество дочерних узлов равно L, а количество элементов данных равно D, то: L = D + 1

　　

Конечный узел (нижняя строка на рисунке выше) не имеет дочерних узлов, но может содержать один, два или три элемента данных. Пустые узлы не будут существовать.

Очень важным моментом в древовидной структуре является соотношение значения ключа между узлами. В двоичном дереве все узлы со значением ключа меньше определенного значения узла находятся в поддереве с корневым левым дочерним узлом этого узла, а все узлы со значением ключа больше определенного значения узла находятся в правом дочернем узле этого узла. Корень на поддереве. Правило дерева 2-3-4 такое же, и добавляются следующие пункты:

Для удобства описания используйте цифры от 0 до 2 для нумерации элементов данных и цифры от 0 до 3 для нумерации дочерних узлов, как показано ниже:

　　

Value Значение ключа всех дочерних узлов поддерева, корнем которого является child0, меньше, чем key0;

Value Значение ключа всех дочерних узлов поддерева, корнем которого является child1, больше, чем key0, и меньше, чем key1;

Value Значение ключа всех дочерних узлов поддерева, корнем которого является child2, больше, чем key1, и меньше, чем key2;

The. Значение ключа всех дочерних узлов поддерева, корнем которого является child3, больше, чем key2.

Упрощенная взаимосвязь показана на следующем рисунке: поскольку дублированные значения ключей обычно не допускаются в дереве 2-3-4, нет необходимости рассматривать случай сравнения одинаковых значений ключей.

2-3-дерево. Наивная реализация +34

Недавно мне понадобилось написать 2-3-дерево и я начал искать информацию в русскоязычном интернете. К сожалению, ни на хабре, ни на других ресурсах я не смог найти достаточно полную информацию на русском языке. На всех ресурсах было одно и то же: свойства дерева, как вставляются ключи в дерево, поиск в дереве и иногда простой пример, как удаляется ключ из дерева; не было реализации.Поэтому, после того, как я сделал то, что мне нужно, решил написать данную статью. Думаю, кому-нибудь будет полезна в образовательных целях, так как на практике обычно реализуют эквивалент 2-3- и 2-3-4-деревьев —.

вводная часть

те, кто знают, что такое двоичное дерево поиска и его недостатки, могут листать дальше — ничего нового здесь не будет.большинству программистов (и не только) известно такое дерево как. у этого дерева очень простые свойства:

• Оба поддерева — левое и правое — являются двоичными деревьями поиска.
• У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных самого узла X.
• В то время, как значения ключей данных у всех узлов правого поддерева (того же узла X) больше либо равно, нежели значение ключа данных узла X.

Деревья поиска используют тогда, когда нужно очень часто выполнять операцию поиск. В обычном дереве поиска есть очень большой недостаток: когда на вход получаем отсортированные данные, наше дерево становится обычным массивом:И тогда операция поиск будет осуществляться за такую же сложность, как и в массиве, — за O(n), где n — количество элементов в массиве.Есть несколько способов, как можно обычное дерево сделать сбалансированным (поиск имеет сложность O(log n)). Об этом очень хорошо написано в двух статьях от хабраюзера:и.

общие свойства 2-3-дерева

определение из wiki:2-3-дерево — структура данных, являющаясястепени 1, страницы которого могут содержать только 2-вершины (вершины с одним полем и 2 детьми) и 3-вершины (вершины с 2 полями и 3 детьми). листовые вершины являются исключением — у них нет детей (но может быть одно или два поля). 2-3-деревья сбалансированы, то есть, каждое левое, правое, и центральное поддерево имеет одну и ту же высоту, и, таким образом, содержат равные (или почти равные) объемы данных.свойства:

• Все нелистовые вершины содержат одно поле и 2 поддерева или 2 поля и 3 поддерева.
• Все листовые вершины находятся на одном уровне (на нижнем уровне) и содержат 1 или 2 поля.
• Все данные отсортированы (по принципу двоичного дерева поиска).
• Нелистовые вершины содержат одно или два поля, указывающие на диапазон значений в их поддеревьях. Значение первого поля строго больше наибольшего значения в левом поддереве и меньше или равно наименьшему значению в правом поддереве (или в центральном поддереве, если это 3-вершина); аналогично, значение второго поля (если оно есть) строго больше наибольшего значения в центральном поддереве и меньше или равно, чем наименьшее значение в правом поддереве. Эти нелистовые вершины используются для направления функции поиска к нужному поддереву и, в конечном итоге, к нужному листу. ( прим. Это свойство не будет выполняться, если у нас есть одинаковые ключи. Поэтому возможна ситуация, когда равные ключи находятся в левом и правом поддеревьях одновременно, тогда ключ в нелистовой вершине будет совпадать с этими ключами. Это никак не сказывается на правильности работы и производительности алгоритма. ).

Структуры данных в с. 9 структур данных C++, которые нужно знать на собеседовании по кодированию

Структуры данных — это форматы, используемые для организации, хранения и изменения данных. Структуры данных являются фундаментальным компонентом информатики и разработки программного обеспечения. Их можно реализовать на любом языке программирования, включая язык программирования C ++. Если вам предстоит собеседование по кодированию, ожидается, что вы будете знать, как использовать структуры данных для эффективной работы с данными.

Сегодня мы рассмотрим структуры данных C ++, которые вам нужно знать на собеседовании по кодированию.

Что такое структуры данных C ++?

Структуры данных — это форматы, используемые для организации, хранения и управления данными. Вы можете использовать структуры данных для эффективного доступа и изменения данных. Существуют различные типы структур данных. Тип, который вы используете, будет зависеть от используемого вами приложения. Каждая структура данных имеет свои преимущества и недостатки.

Структуры данных обычно подпадают под эти две категории:

• Линейные структуры данных: элементы расположены последовательно (например, массивы, связанные списки, стеки, очереди)
• Нелинейные структуры данных: элементы не располагаются последовательно, а хранятся на разных уровнях (например, деревья, графики).

9 структур данных C ++, которые нужно знать перед собеседованием

1. Массивы

Массив — это последовательный список значений. Вы можете использовать массивы для хранения и доступа к нескольким значениям одного и того же типа данных под одним идентификатором. Массивы упрощают выполнение операций со всем набором данных. Они также отлично подходят для получения данных.

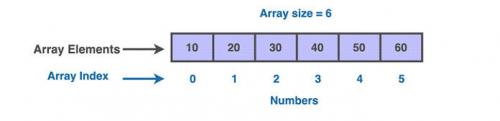
Есть одномерные массивы и многомерные массивы. Значения, хранящиеся в массиве, называются элементами. Элементы хранятся в последовательных блоках памяти, называемых индексами. Размер массива определяется количеством содержащихся в нем элементов. На фото — одномерный массив размером шесть.

Общий синтаксис для инициализации одномерного массива:

ArrayName = значение;

В этом коде мы инициализируем массив с именем, Exampleкоторый хранит 200 по индексу 0и 201 по индексу 1.

2. Графики

Графики — это нелинейные структуры данных. Они состоят из конечного набора вершин (то есть узлов), соединенных набором ребер. Порядок графа относится к количеству вершин в графе. Размер графа соответствует количеству его ребер.

На этой иллюстрации представлены вершины и ребра. Граф также представляет собой циклический граф. Граф является циклическим, если хотя бы один узел имеет путь, который ведет обратно к самому себе.

Графики часто используются для моделирования реальных отношений в различных контекстах, от социальных сетей до нейронных сетей.

Есть три распространенных типа графиков:

• Ненаправленные графы: граф, в котором все ребра двунаправлены.
• Направленные графы: граф, в котором все ребра однонаправлены.
• Взвешенные графы: граф, в котором всем ребрам присвоено значение, называемое весом.

Скорее всего, на собеседовании вас попросят просмотреть график.

3. Связанные списки

Связанные списки — это линейные структуры данных, состоящие из набора узлов, представляющих последовательность. Каждый узел содержит значение и указатель на следующий узел в последовательности. Связанные списки отлично подходят для добавления и удаления узлов. Однако они не подходят для извлечения узлов, поскольку каждый узел знает только об узле рядом с ним.

Существуют как односвязные списки, так и двусвязные списки. Односвязный список — это самая основная форма связанного списка, где каждый узел знает только о следующем узле в последовательности. В двусвязном списке каждый узел указывает на узел, предшествующий и следующий за ним в последовательности. Направление этих ссылок часто бывает «вперед» и «назад», «следующее» и «предыдущее».

Убедитесь, что вы знаете, как перевернуть связанный список, прежде чем идти на собеседование по C ++.

Алгоритмы и структуры данных статья. Для кого написана эта статья про Алгоритмы

Если ты вообще не понимаешь ничего в программировании и хочешь с чего-то начать, но не знаешь с чего именно, то информация, которую ты здесь получишь, станет хорошим «entry point» в мир разработки.

Если ты учишься и мечтаешь стать хорошим программистом, то материал который будет освещен — именно для тебя.

Если ты уже хороший программист и хочешь стать еще и лучшим, то темы, которые будут раскрыты, тебе пригодятся.

Если ты уже senior-помидор, гуру программирования и познал «дзен», то бери свой кофе, садись поудобнее и проверь, не заржавел ли еще и помнишь ли азы.

Если ты готовишься к собеседованию в топ компанию — этот материал поможет тебе в подготовке.

Если ты хочешь зарабатывать больше — твоя прибыль вырастет, потому что работодатели ценят людей с такими знаниями.

Если ты хочешь решать действительно тяжелые и интересные задачи, где надежность и производительность являются ключевыми — написанное именно для тебя.

Данную статью можно использовать как для обучения, так и в качестве пособия, к которому возвращаешься, чтобы подсмотреть в случае, если забыл или сомневаешься, какую структуру данных выбрать или если знаешь точно, какую, но не помнишь, как именно ее эффективно применить.

Также, это хорошая практика языка программирования С++, потому что я буду использовать его в своих примерах. Кто думает, что это тяжелый язык, увидит — не такой страшный монстр, как его рисуют. Но сразу скажу: я не буду подробно останавливаться на тонкостях С++ ( шпаргалка по C++ ). Нужно понимать, что различные подходы, алгоритмы и структуры данных не зависят от языка.

Поэтому ты можешь делать все то же самое, но использовать комфортный язык программирования вместо предложенного.

Структура данных очередь.

О́чередь  — абстрактный тип данных с дисциплиной доступа к элементам «первый пришёл — первый вышел» ( FIFO , англ.   first in, first out ). Добавление элемента (принято обозначать словом enqueue — поставить в очередь) возможно лишь в конец очереди, выборка — только из начала очереди (что принято называть словом dequeue — убрать из очереди), при этом выбранный элемент из очереди удаляется.

Существует несколько способов реализации очереди в языках программирования.

Первый способ представляет очередь в виде массива и двух целочисленных переменных start и end.

Обычноstartуказывает на голову очереди,end — на элемент, который заполнится, когда в очередь войдёт новый элемент. При добавлении элемента в очередь вqзаписывается новый элемент очереди, аendуменьшается на единицу. Если значение end становится меньше 1, то мы как бы циклически обходим массив, и значение переменной становится равным n. Извлечение элемента из очереди производится аналогично: после извлечения элементаqиз очереди переменнаяstartуменьшается на 1. С такими алгоритмами одна ячейка изnвсегда будет незанятой (так как очередь сnэлементами невозможно отличить от пустой), что компенсируется простотой алгоритмов.

Преимущества данного метода: возможна незначительная экономия памяти по сравнению со вторым способом; проще в разработке.

Недостатки: максимальное количество элементов в очереди ограничено размером массива. При его переполнении требуется перевыделение памяти и копирование всех элементов в новый массив.

Второй способ основан на работе с динамической памятью. Очередь представляется в качестве линейного списка , в котором добавление/удаление элементов идет строго с соответствующих его концов.

Преимущества данного метода: размер очереди ограничен лишь объёмом памяти.

Недостатки: сложнее в разработке; требуется больше памяти; при работе с такой очередью память сильнее фрагментируется; работа с очередью несколько медленнее.

 Процедура enqueue( x ):
 S1.push( x )

 Функция dequeue(): если S2 пуст: если S1 пуст:
 сообщить об ошибке: очередь пуста

 пока S1 не пуст:
 S2.push(S1.pop())

 вернуть S2.pop()

Такой способ реализации наиболее удобен в качестве основы для построения персистентной очереди .

Практически во всех развитых языках программирования реализованы очереди. В CLI для этого предусмотрен класс System.Collections.Queue с методами Enqueue и Dequeue. В STL также присутствует класс queue, определённый в заголовочном файле queue. В нём используется та же терминология (push и pop), что и в стеках .

Очередь в программировании используется, как и в реальной жизни, когда нужно совершить какие-то действия в порядке их поступления, выполнив их последовательно. Примером может служить организация событий в Windows. Когда пользователь оказывает какое-то действие на приложение, то в приложении не вызывается соответствующая процедура (ведь в этот момент приложение может совершать другие действия), а ему присылается сообщение, содержащее информацию о совершенном действии, это сообщение ставится в очередь, и только когда будут обработаны сообщения, пришедшие ранее, приложение выполнит необходимое действие.

Клавиатурный буфер BIOS организован в виде кольцевого массива, обычно длиной в 16 машинных слов, и двух указателей: на следующий элемент в нём и на первый незанятый элемент.

Типы данных и структуры данных. Алгоритмы

Алгоритм — такое хитроумное название для последовательности совершаемых действий.Структуры данных реализованы с помощью алгоритмов, алгоритмы — с помощью структур данных. Всё состоит из структур данных и алгоритмов, вплоть до уровня, на котором бегают микроскопические человечки с перфокартами и заставляют компьютер работать. (Ну да, у Интела в услужении микроскопические люди. Поднимайся, народ!)Любая данная задача реализуется бесконечным количеством способов. Как следствие, для решения распространённых задач изобрели множество различных алгоритмов.Например, для сортировки неупорядоченного множества элементов существует до смешного большое количество алгоритмов:

Сортировка вставками, Сортировка выбором, Сортировка слиянием, Сортировка пузырьком, Cортировка кучи, Быстрая сортировка, Сортировка Шелла, Сортировка Тима, Блочная сортировка, Поразрядная сортировка…

Некоторые из них значительно быстрее остальных. Другие занимают меньше памяти. Третьи легко реализовать. Четвёртые построены на допущениях относительно наборов данных.Каждая из сортировок подходит лучше других для определённой задачи. Поэтому вам надо будет сперва решить, какие у вас потребности и критерии, чтобы понять, как сравнивать алгоритмы между собой.Для сравнения производительности алгоритмов используется грубое измерение средней производительности и производительности в худшем случае, для обозначения которых используется термин «О» большое.

2 3 куча. ОЧЕРЕДИ. ОЧЕРЕДИ С ПРИОРИТЕТОМ.

Стр 1 из 5 Следующая ⇒

ВВЕДЕНИЕ. 4

1 ЗАДАЧИ НА ГРАФАХ.. 5

2 ОЧЕРЕДИ. ОЧЕРЕДИ С ПРИОРИТЕТОМ.. 6

2.1 Основные подходы к реализации очередей. 7

2.2 Основные подходы к реализации очередей с приоритетом. 9

2.2.1 Бинарная куча………………………………………………………………………. 10

2.2.2 Биномиальная куча. 12

2.2.3 Куча Фибоначчи. 14

3 СТРУКТУРА ДАННЫХ 2-3 КУЧА.. 16

3.1 Вставка в кучу. 19

3.2 Извлечение приоритетного элемента из кучи. Поиск. Слияние. 23

3.3 Изменение ключа произвольного элемента кучи. 25

3.4 Обход по куче. 27

4 СРАВНИТЕЛЬНЫЙ АНАЛИЗ ОЧЕРЕДЕЙ С ПРИОРИТЕТОМ.. 28

5 ОПТИМИЗАЦИЯ АЛГОРИТМОВ НА ГРАФАХ.. 31

5.1 Алгоритм Дейкстры.. 31

5.2 Алгоритм Прима. 34

ПОДВЕДЕНИЕ ИТОГОВ.. .36

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. .37

ПРИЛОЖЕНИЕ А : ИНТЕРФЕЙС РЕАЛИЗАЦИЙ ОЧЕРЕДЕЙ С ПРИОРИТЕТОМ

ПРИЛОЖЕНИЕ Б : ЛИСТИНГИ ОСНОВНЫХ ОПЕРАЦИЙ 2-3 КУЧИ

ВВЕДЕНИЕ

В компьютерных науках и программировании в целом очень важны быстродействие алгоритмов и их надежность, а если излагаться конкретнее, то необходимы оптимизации, которые ведут к ускорению работы алгоритма, уменьшению требования к ресурсам и при этом сохраняя уровень надежности на должном уровне. Вопрос оптимизации алгоритмов очень многогранен, поэтому целью моей работы будет оптимизация алгоритмов на графах, а точнее оптимизация определенного класса задач на графах. Оптимизация, изложенная в этой работе будет существенно ускорять выбор из множества (например, выбор ближайшего города в алгоритме Дейкстры для поиска кратчайшего пути). В этой работе будут кратко описаны некоторые родственные понятия, но описаны они будут на минимальном уровне, чтобы обеспечивать связь между понятиями. Далее будут рассмотрены основные подходы к реализации очередей с приоритетом, описание 2-3 кучи, сравнительный анализ.

ЗАДАЧИ НА ГРАФАХ

Графы повсеместно используются в информатике для задач, связанных с взаимным расположением объектов, или сводимым к ним задач.

Приведем пример задач, которые решаются на графах:

· Поиск кратчайшего пути между парой вершин

· Поиск Гамильтонова цикла минимального веса в графе.

· Поиск минимального ациклического подграфа, которые включает в себя все вершины (поиск минимального остового дерева).

Мною не случайно были выбраны именно эти алгоритмы. Дело в том, что решение каждой из этих задач подразумевает выбор из множества некоторого самого оптимального решения для следующей итерации.

Например, для первой задачи можно использовать алгоритм Дейкстры и тогда нам будет необходимо на каждой итерации выбирать вершину, которая не была выбрана и ближе всего к начальной.

Для второй задачи (задача Коммивояжера) необходимо определять кратчайший путь между текущей вершиной, и множеством ещё не пройденных вершин при решении задачи алгоритмом выбора ближайшего соседа.

Для последней задачи можно использовать алгоритм Прима, где также необходимо получать минимальные пути от любой вершины из множества выбранных, до ближайшей из множества не выбранных.

Эти задачи (в которых необходимо выбирать оптимальное значение из множества) мы отнесем в отдельный класс. Данная работа направлена на оптимизацию именно этого класса задач на графах.

В каждом случае при решении в лоб мы должны на каждой итерации дополнительно тратить n итераций для определения минимума. Было бы не плохо иметь структуру данных, которая позволила бы получать значение минимума быстрее чем за линейное время (в идеале за константное). И в этом нам помогут очереди, а точнее очереди с приоритетом.

Структуры данных в программировании. Массивы

Это наипростейшие и широко используемые структуры данных, в которых элементы следуют один за другим. Представляет собой контейнер, в котором может храниться фиксированное количество однотипных компонентов.

Важнейшие термины:

• элементами называют все компоненты, хранящиеся в массиве;
• индексы – местонахождение каждого элемента в массиве выражается целым числовым индексом, используемом для его идентификации.

Размерность массива определяет количество индексов в нем. Они бывают одномерными (называют векторами) и многомерными (массив в середине массива). Массивы могут объявляться разными способами на различных языках программирования.

Некоторые структуры являются производными массивов (стеки, очереди). В массиве каждый элемент имеет индекс (положительное целое числовое значение), соответствующий тому, какую позицию в массиве он занимает.

Язык программирования определяет, с какого значения в массиве начинается нумерация. Во многих языках начальным индексом массива определен 0.

Массивы бывают:

• статическими — характеризуются однородностью данных;
• динамическими – характеризуются непостоянством размера, который может меняться в ходе выполнения программы. Это усложняет процесс, ухудшает быстроту действий, но работа с информацией становится более гибкой;
• гетерогенными – характеризуется неоднородностью данных.

Основные операции, которые поддерживаются массивами:

• Traverse – выставляет один за одним все компоненты массива;
• Insert – добавляет один или несколько элементов по указанному индексу;
• Get – производит возврат элемента по указанному индексу;
• Delete – выполняет удаление элемента по указанному индексу;
• Size – позволяет узнать общую численность элементов, содержащихся в массиве.

Основные структуры данных. 8 известных структур данных, о которых спросят на собеседовании

Кратко разбираем 8 основных структур данных, в которых должен разбираться каждый разработчик. Проверьте свои теоретические знания.

Никлаус Вирт, швейцарский информатик, написал в 1976 году книгу под названием «Алгоритмы + структуры данных = программы».

Больше сорока лет спустя это уравнение все еще верно. Почти все задачи программирования требуют от разработчика глубокого понимания структур данных. Вопросы на эту тему обязательно встречаются на любом IT-собеседовании.

Иногда в этих вопросах явно упоминается искомая структура, например, «дано двоичное дерево». В других случаях это не столь очевидно, например, «мы хотим отслеживать количество книг, связанных с каждым автором».

Изучение структур данных имеет важное значение, даже если вы не ищете новую работу, а просто хотите улучшить текущую. Давайте начнем с понимания основ.

Что такое структуры данных?

Простыми словами, структура данных – это контейнер, который хранит информацию в определенном виде. Из-за такой «компоновки» она может быть эффективной в одних операциях и неэффективной в других. Цель разработчика – выбрать из существующих структур оптимальный для конкретной задачи вариант.

Зачем нужны структуры данных?

Данные являются самой важной сущностью в информатике, а структуры позволяют хранить их в организованной форме.

Какую бы проблему вы не решали, вам приходится иметь дело с данными — будь то зарплата сотрудника, цены на акции, список покупок или даже простой телефонный справочник.

В зависимости от ситуации данные должны храниться в некотором определенном формате. Структуры данных предлагают несколько вариантов таких размещений.

8 часто используемых структур

Давайте сначала перечислим наиболее часто используемые структуры данных, а затем рассмотрим их одну за другой:

1. Массив (Array)
2. Стек (Stack)
3. Очередь (Queue)
4. Связный список (Linked List)
5. Дерево (Tree)
6. Граф (Graph)
7. Префиксное дерево (Trie)
8. Хэш-Таблица (Hash Table)

Массивы

Массив – это самая простая и наиболее широко используемая из структур. Стеки и очереди являются производными от массивов.

Вот изображение простого массива размером 4, содержащего элементы (1, 2, 3 и 4).

Каждому из них присваивается неотрицательное числовое значение – индекс, который соответствует позиции этого элемента в массиве. Большинство языков определяют начальный индекс массива как 0.

Существует два типа массивов:

• Одномерные массивы (как на картинке).
• Многомерные массивы (массивы массивов).

Основные операции с массивами

• Insert – вставка.
• Get – получение элемента.
• Delete – удаление.
• Size – получение общего количества элементов в массиве.

Частые вопросы о массивах

• Найти второй минимальный элемент.
• Первые не повторяющиеся целые числа.
• Переставить положительные и отрицательные значения.

Стеки

Мы все знакомы с опцией Отменить (Undo), которая присутствует практически в каждом приложении. Вы когда-нибудь задумывались, как это работает?

Для этого вы сохраняете предыдущие состояния приложения (определенное их количество) в памяти в таком порядке, что последнее сохраненное появляется первым. Это не может быть сделано только с помощью массивов. Здесь на помощь приходит стек.

Пример стека из реальной жизни – куча книг, лежащих друг на друге. Чтобы получить книгу, которая находится где-то в середине, вам нужно удалить все, что лежит сверху. Так работает метод LIFO (Last In First Out, последним пришел – первым ушел).

Вот изображение стека, содержащего три элемента (1, 2 и 3). Элемент 3 находится сверху и будет удален первым:

Основные операции со стеками

• Push – вставка элемента наверх стека.
• Pop – получение верхнего элемента и его удаление.
• isEmpty – возвращает true, если стек пуст.
• Top – получение верхнего элемента без удаления.

Часто задаваемые вопросы о стеках

• Вычисление постфиксного выражения с помощью стека.
• Сортировка значений в стеке.

Очереди

Как и стек, очередь – это линейная структура данных, которая хранит элементы последовательно. Единственное существенное различие заключается в том, что вместо использования метода LIFO, очередь реализует метод FIFO (First in First Out, первым пришел – первым ушел).

Идеальный пример этих структур в реальной жизни – очереди людей в билетную кассу. Если придет новый человек, он присоединится к линии с конца, а не с начала. А человек, стоящий впереди, первым получит билет и, следовательно, покинет очередь.