Структура данных 2-3-4 дерева и 2-3 дерева. Введение 2-3-4 дерева
- Структура данных 2-3-4 дерева и 2-3 дерева. Введение 2-3-4 дерева
- Авл-дерево. Для чего нужны АВЛ-деревья
- Бинарное дерево —, что это? B-деревья
- 2-3 дерево C++. 2-3 Trees - Data Structures and Algorithms in C++
- 2-3 дерево java. 2 Как «2-3 дерева» поддерживают абсолютный баланс?
- Реализация словаря 2 3 деревьями. АТД Словарь. Реализация словаря 2-3 деревьями.
- 2-3 дерево онлайн. 2-3-дерево
Структура данных 2-3-4 дерева и 2-3 дерева. Введение 2-3-4 дерева
Каждый узел в дереве 2-3-4 имеет максимум четыре байтовых точки и три элемента данных. Числовое значение 2, 3 и 4 в имени относится к числу дочерних узлов, которые может содержать узел. Существует три возможных сценария для неконечных узлов:
① узел с элементом данных всегда имеет два дочерних узла;
② узел с двумя элементами данных всегда имеет три дочерних узла;
③ узел с тремя элементами данных всегда имеет четыре дочерних узла;
Короче говоря, число дочерних узлов неконечного узла всегда на 1 больше, чем элементов данных, которые он содержит. Если количество дочерних узлов равно L, а количество элементов данных равно D, то: L = D + 1
Конечный узел (нижняя строка на рисунке выше) не имеет дочерних узлов, но может содержать один, два или три элемента данных. Пустые узлы не будут существовать.
Очень важным моментом в древовидной структуре является соотношение между размером значения ключа между узлами. В двоичном дереве все узлы со значением ключа меньше определенного значения узла находятся в поддереве с корневым левым дочерним узлом этого узла, а все узлы со значением ключа больше определенного значения узла находятся в правом дочернем узле этого узла. Корень на поддереве. Правило дерева 2-3-4 такое же, и добавляются следующие пункты:
Для удобства описания используйте цифры от 0 до 2 для нумерации элементов данных и цифры от 0 до 3 для нумерации дочерних узлов, как показано ниже:
Value Значение ключа всех дочерних узлов поддерева, корнем которого является child0, меньше, чем key0;
② значение ключа всех дочерних узлов поддерева, корнем которого является child1, больше, чем key0, и меньше, чем key1;
Value Значение ключа всех дочерних узлов поддерева, корнем которого является child2, больше, чем key1, и меньше, чем key2;
Value. Значение ключа всех дочерних узлов дочернего дерева, корнем которого является child3, больше, чем key2.
Упрощенная взаимосвязь показана на следующем рисунке: поскольку дублированные значения ключей обычно не допускаются в дереве 2-3-4, нет необходимости рассматривать случай сравнения одинаковых значений ключей.
Авл-дерево. Для чего нужны АВЛ-деревья
Для хранения данных. Эта структура позволяет хранить информацию в «узлах» дерева и перемещаться по ней с помощью путей, которые соединяют между собой узлы. Благодаря особому алгоритму данные хранятся относительно эффективно и с ними довольно удобно работать. Мы подробнее поговорим об этом ниже.
Для поисковых алгоритмов. АВЛ-деревья и бинарные деревья поиска в принципе — важная составная часть разнообразных алгоритмов поиска информации. Их применяют при построении поисковых систем и интеллектуальных сервисов.
Для сортировки. Хранение информации в АВЛ-дереве позволяет быстрее отсортировать данные, а задача сортировки часто встречается в IT. С помощью деревьев можно хранить и сортировать информацию в базах данных, в особых участках памяти, в хэшах и других структурах.
Для программных проверок. АВЛ-дерево может использоваться для решения некоторых стандартных задач, например для быстрой проверки существования элемента в структуре.
Для построения сложных структур. Дерево может быть составной частью более сложной структуры данных или какого-либо алгоритма, например используемого для поиска, хранения или принятия решений.
Для других задач. Деревья могут понадобиться везде, где нужны связные структуры данных, оптимизированные под определенные операции. Например, они могут быть более функциональной альтернативой связанному списку — линейной структуре данных, где в каждом элементе есть ссылка на предыдущий и/или следующий.
Бинарное дерево —, что это? B-деревья
Статья расскажет о том, что такое бинарные деревья . Будут представлены способы их представления и основные термины. Отдельное внимание будет уделено B-дереву и его отличию от двоичных структур.
Деревом называют структуру данных, которая имеет древовидный вид, то есть характеризуется наличием набора связанных узлов. Бинарное дерево — это конечное множество элементов, связанных с двумя разными бинарными деревьями — правым и левым поддеревьями.
Способ представления:
На что следует обратить внимание: — А — корень дерева; — B — корень левого поддерева и предок D; — С — корень правого поддерева; — D — потомок родительского узла B; если D располагается на уровне i, то B – на уровне i-1.
Необходимо выделить следующие термины: — узел (вершина) — это каждый элемент бинарного дерева; — ветви — связи между узлами; — глубина (высота) — наибольший уровень какого-нибудь элемента; — лист (терминальный узел) — термин применяется, если элемент не имеет потомков; — внутренние узлы — узлы ветвления; — степень внутреннего узла — число его потомков (наибольшая степень всех существующих узлов — это степень всего бинарного дерева); — длина пути к x — количество ветвей, которые необходимо пройти от корня до текущего узла x. Длина пути самого корня равна нулю, а узел на уровне i обладает длиной пути, которая равна i.
Использование
На практике бинарные деревья применяются, когда в каждой точке какого-нибудь вычислительного процесса нужно принимать одно из 2-х возможных решений. Существует множество задач, решаемых таким способом. Одна из них — выполнение операции, условно говоря, X с каждым элементом дерева. X рассматривается в качестве параметра обобщенной задачи посещения всех вершин либо задачи обхода дерева. Если рассмотреть такую задачу в качестве единого последовательного процесса, то можно сказать, что отдельные вершины посещаются в определенном порядке, то есть могут считаться линейно расположенными.
Способы обхода
Предположим, что имеется дерево (не пустое), в котором A является корнем, а B и C — левым и правым поддеревьями.
Есть 3 способа обхода: 1. Обход в прямом порядке — сверху вниз: A, B, C — префиксная форма. 2. Обход слева направо (симметричный порядок): B, A, C — инфиксная форма. 3. Обход снизу вверх (обратный порядок): B, C, A — постфиксная форма.
Реализация
На практике вершину древа можно описать в качестве структуры:
Тогда обход в префиксной форме будет выглядеть следующим образом:
Теперь инфиксная форма:
И постфиксная:
Бинарное дерево поиска
Оно представляет собой двоичное (бинарное) дерево, для которого справедлив ряд дополнительных условий. Эти условия называют свойствами:
Данные в каждой вершине должны обладать ключами, где определена операция сравнения “
Обычно информация, которая представляет каждую вершину, — это запись, а не единственное поле данных.
Чтобы составить бинарное дерево поиска, пригодится функция добавления узла:
Удаляем поддерево
B-дерево. Поиск по B-дереву
В бинарном дереве поиска каждый узел содержит лишь одно значение (ключ) и не более 2-х потомков. Но существует особый вид древа поиска, называемый B-дерево (Би-дерево). Здесь узел содержит больше одного значения и больше 2-х потомков. Также его называют сбалансированным по высоте деревом поиска порядка m (Height Balanced m-way Search Tree).
B-дерево представляет собой сбалансированное дерево поиска, где каждый узел содержит много ключей и имеет больше 2-х потомков.
Возможные операции: 1. Поиск. 2. Вставка (вставляем новый элемент). 3. Удаление.
Каждое B-дерево имеет порядок. Для примера рассмотрим B-дерево порядка m. Оно будет обладать рядом следующих характеристик:
Ниже можно посмотреть на B-дерево четвертого порядка, содержащее максимум три значения ключа и максимум четыре потомка для каждой вершины.
Поиск аналогичен поиску по двоичному дереву. Следует вспомнить, что в двоичном древе поиск начинается с корня, причем каждый раз принимается 2-стороннее решение (пойти по правому поддереву либо по левому). В В-дереве поиск тоже начинается с корневого узла, но с той лишь разницей, что на каждом шаге принимается не 2-стороннее, а n-стороннее решение, причем n для дерева в данном случае представляет общее число потомков рассматриваемого узла. Сложность поиска такого дерева — O(log n).
Алгоритм следующий:
Также существует такое понятие, как вставка в B-дерево.
2-3 дерево C++. 2-3 Trees - Data Structures and Algorithms in C++
A 2-3 Tree is a type of tree in data structures in which every node of the tree is either a 2 node
or 3 nodes. It is a special type of B-Tree with order 3.
A 2 node in the tree is one which has one data part and two child nodes.
A 3 node in the tree is one which has two data parts and three child nodes.
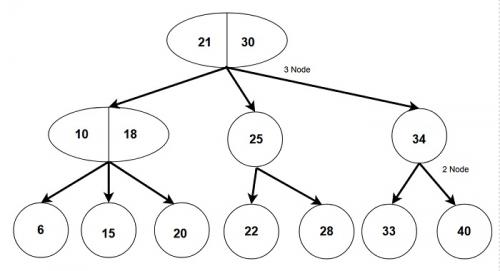
Fig:- A 2-3 tree
Properties of a 2-3 Tree:-
Every internal node is either a 2 node or a 3 node.
A node containing one data part can be a 2 node with exactly 2 children or a leaf node with no children.
A node containing two data parts can only be a 3 node with exactly 3 children.
All leaf nodes are always at the same level.
A 2-3 tree is always a height balanced tree.
Search operations are fast and efficient in a 2-3 tree.
2 Node:-
Exactly two children.
Left child with smaller weight.
Right child with greater weight.
Can be a leaf node with no child.
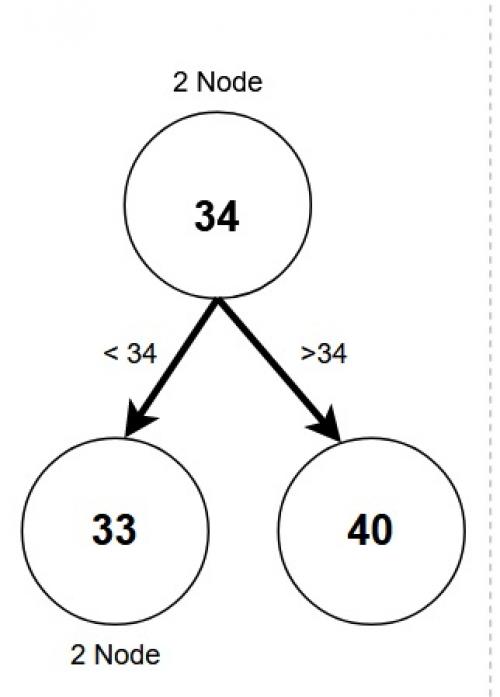
3 Node:-
Exactly three children.
2 data values.
Left child with weight smaller than left data value.
Middle child with weight in between both data values.
Right child with weight greater than right data value.
Can never be a leaf node.
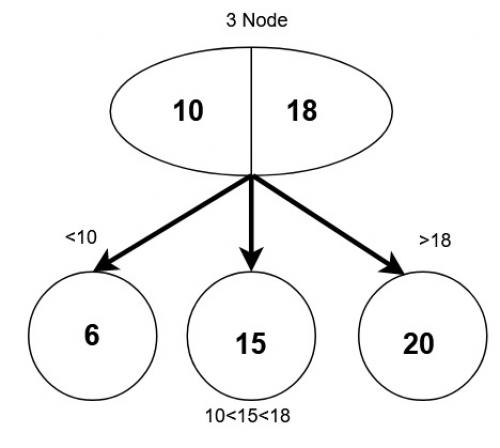
Operations in a 2-3 Tree:-
1. Searching in a 2-3 tree
Similar to the search operation in a binary search tree as the data is sorted.
To search X in a 2-3 tree.
If tree is empty → return False
If we reach root node then return False (not found)
If X is less than the left data part, then search the left subtree
If X is greater than left data and more than right data, search the middle subtree.
If X is greater than the right data part, then search right subtree.
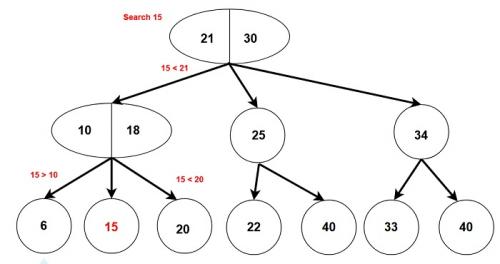
2. Inserting a node in a 2-3 tree
To insert X in a 2-3 tree.
If the tree is empty → Add X as root.
Search for the right position of X and add it as a leaf node.
If there is a leaf node with one data part, add X with and leaf node becomes 2 - Node.
If the leaf node has two data parts, add X. Split temporary 3-nodes and move data to parent nodes according to the sorting order.
Make 2-3 tree and add nodes in order → 10, 5, 8, 15, 23, 21
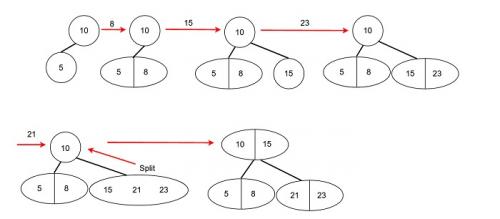
3. Deletion of a node in a 2-3 tree
To delete X in a 2-3 tree.
If the tree is empty return false.
Search for the position of X and delete it, then adjust the tree.
If X is part of 3 node delete X and adjust left value and middle value. Also adjust node’s ancestor’s left and middle value if necessary.
If X is part of 2 node then adjust and split the tree in a recursive manner arranging nodes in sorted order.
2-3 дерево java. 2 Как «2-3 дерева» поддерживают абсолютный баланс?
Чтобы сохранить баланс между 2-3 деревьями, давайте посмотрим, как добавить элементы в 2-3 дерева.
Сначала мы добавляем узел к пустому дереву, тогда этот узел, несомненно, является корневым узлом, и это узел 2. А что, если мы добавим к нему еще один узел?
Как показано на рисунке выше, мы добавляем элемент 7 в дерево 2-3. В предыдущем дереве двоичного поиска мы помещали 7 в правое поддерево корневого узла, которое не может поддерживаться. Абсолютный баланс дерева. В дереве 2-3 мы не можем добавлять элементы в пустые узлы, поэтому элементы будут объединены с 2 узлами в 3 узла.
, а затем мы добавляем к нему элементы
Поскольку мы не можем добавлять элементы в пустые узлы, мы также сначала объединяем элемент 1 с нашим корневым узлом, потому что в это время корневой узел уже является 3 узлом, а 2-3 В дереве нет 4 узлов, поэтому сначала формируем временные 4 узла.
Корневой узел в настоящее время не соответствует определению дерева 2-3, поэтому нам нужно разделить 4 узла в это время, чтобы сделать из них три 2 узла
Это снова соответствует определению 2-3 дерева, и теперь мы добавляем в него элементы.
11 больше 3, из-за природы двоичного дерева поиска его нужно добавить в правое поддерево, 11 больше 7, и его нужно добавить в его правое поддерево, правое поддерево Пусто, из-за природы дерева 2-3, вы не можете добавлять элементы к пустому узлу, поэтому он объединяется с узлом 2 из 7, чтобы сформировать узел 3
Теперь мы добавляем в него элементы
Согласно предыдущей операции, мы легко должны знать, как добавить
В настоящее время наше 2-3-е дерево неуравновешено, что нам делать? Сделаем еще одну операцию, чтобы объединить узел, в котором расположен элемент 11, и узел, в котором расположен элемент 3, в тройной узел.
Дерево 2-3 постоянно выполняет такие операции для поддержания своего абсолютного баланса.
Реализация словаря 2 3 деревьями. АТД Словарь. Реализация словаря 2-3 деревьями.
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15 16 17
- 18
- 19
- 20
- 21
- 22
- Далее ⇒
2-3 деревом называется дерево, в котором каждый внутренний узел имеет двух или трех сыновей, а длины всех путей от корня в листья совпадают между собой. Поскольку в процессе поиска необходимо делать выбор между тремя сыновьями, в 2-3 дереве каждый внутренний узел дерева хранит не один, а два ключа. Линейно упорядоченное множество S можно представить 2-3 деревом, приписав его элементы листьям дерева с использованием заданного порядка. Каждый внутренний узел v содержит две метки L ( v ) и M ( v ) , где L ( v ) - наибольший элемент, приписанный листьям самого левого сына вершины v , M ( v ) - наибольший элемент, приписанный листьям второго сына этой вершины. Используя эти метки для поиска, легко решить задачу НАЙТИ за время пропорциональное высоте дерева ( O (log( n )) ). 2-3 деревья служат хорошей структурой данных для АТД со следующим набором операций:
1. ВСТАВИТЬ, УДАЛИТЬ, НАЙТИ
2. ВСТАВИТЬ, УДАЛИТЬ, НАЙТИ ЭЛЕМЕНТ С МИНИМАЛЬНЫМ
ЗНАЧЕНИЕМ КЛЮЧА
3. ВСТАВИТЬ, УДАЛИТЬ, ОБЪЕДИНИТЬ, НАЙТИ С МИНИМАЛЬНЫМ
ЗНАЧЕНИЕМ КЛЮЧА
4. ВСТАВИТЬ, УДАЛИТЬ, НАЙТИ, СЦЕПИТЬ, РАСЦЕПИТЬ
Как уже упоминалось выше, АТД с набором операций из множества 1 называется
Словарем, из множества 2 – Очередью с приоритетами, 3 – Сливаемым деревом, 4 –
Сцепляемой очередью.
2-3 деревья позволяют эффективно выполнять последовательности операций из любого набора перечисленных операций. Единственная несовместимость состоит в том, что операция ОБЪЕДИНИТЬ приводит к неупорядоченному множеству, а операции СЦЕПИТЬ, РАСЦЕПИТЬ предполагают наличие порядка.
2-3 дерево онлайн. 2-3-дерево
Чтобы понять красно-чёрное дерево, нужно понять 2-3-дерево.
Забегая вперед, скажу, что 2-3-дерево — это, по сути, родитель нашего КЧД, поэтому важно начать именно с него. Поймем 2-3-дерево — поймём и КЧД.
2-3-дерево — абстрактный тип данных, напоминающий по структуре дерево. В нодах 2-3-дерева может быть одно или два значения и два или три потомка (от чего зависит количество значений и потомков ноды, узнаем ниже). Ноду с одним значением и двумя потомками будем называть 2-нода, ноду с двумя значениями и тремя потомками — 3-нода. Объяснение я начну с создания такого дерева: это наглядно и просто. Но некоторые уточнения всё же нужны:
- Добавляя элемент, мы всегда спускаемся вниз по дереву.
- Дерево отсортировано классически — меньшие значения находятся слева, бОльшие — справа.
- 2-3-дерево — отсортированное, сбалансированное дерево.
Итак, начнём с первой ноды, это число 5. Тут всё просто — 5 становится корнем.

Добавим число 12. Его мы также добавляем в корень (помним, что нода может иметь два значения), но теперь нам нужно отсортировать нашу ноду (сортировать два элемента, ха), т.е. уложить их в порядке возрастания. В итоге получается нода 5-12.

Добавим следующее число. Пусть это будет 17. Давайте пока добавим наш элемент в единственную ноду и снова отсортируем ее. Получилась нода 5-12-17.
Внимательный читатель заметит тут подвох — выше я говорил о том, что наши ноды могут содержать не более двух элементов. Вот тут и происходит магия! Мы берём средний элемент нашей ноды и проталкиваем его наверх. Итог виден на картинке. Корнем стало число 12, левым сыном — число 5, правым — 17.
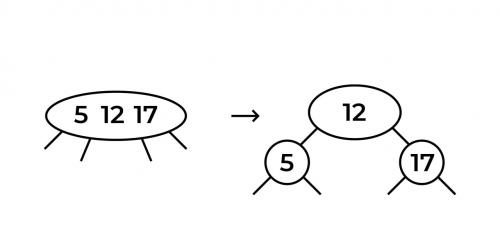
То, что мы сделали выше, можно назвать балансировкой 2-3-дерева. Правило в этой балансировке простое: если в ноде оказывается 3 значения, среднее мы проталкиваем наверх. Алгоритм действий зависит от трёх условий:
- Нода является корнем. Тогда ничего не остаётся, как создать новую ноду с одним значением и сделать её новым корнем (как в нашем случае).
- Родительская нода имеет одно значение. Тогда мы просто добавляем значение к родителю и завершаем балансировку (при этом у родителя появляется третий потомок).
- Родительская нода имеет два значения. Тогда мы снова проталкиваем значение вверх, пока не придём к пункту 1 или 2.