Хранение данных в дереве. Обзор паттернов хранения деревьев в реляционных БД +11

Хранение данных в дереве. Обзор паттернов хранения деревьев в реляционных БД +11

Всем привет! Меня зовут Пантелеев Александр и я бэкенд-разработчик в компании Bimeister.

Постараюсь описать исчерпывающе, кратко и понятно суть основных паттернов хранения деревьев в реляционных базах данных. Надеюсь, что статья будет полезна тем, кто до сего момента не сталкивался с такими паттернами, и станет отправной точкой в их понимании.

В этой статье не будет терминов реляционной алгебры или базы данных: таких как атрибут, домен и т. д. Также не будет привязки к какой-либо СУБД, какому-либо SQL или пользовательскому коду.

Всего существует 4 общепринятых паттерна хранения деревьев:

Adjacency List;

Nested Sets;

Closure Table;

Materialized Path.

Кратко рассмотрим каждый из них.

Adjacency List

Описание

Это самый простой и интуитивный вариант хранения. Каждому элементу сопоставляется его свойство — его родительский элемент. Если родительский элемент не задан, то он считается корневым элементом.Когда связь сопоставления элемента и родительского элемента хранится отдельно от элемента, Adjacency List можно рассматривать как частный случай Closure Table со связями 1 уровня.

Преимущества

Лёгкость реализации, а также простота вставки, удаления и перемещения элементов в дереве.

Недостатки

Можно получить только непосредственные дочерние элементы. Чтобы получить все дочерние элементы, необходимо выполнить рекурсивный запрос либо производить множественные запросы.

Примеры

его дочерние элементы, нам необходимо выбрать элементы, удовлетворяющие условию:

равен «B»

Nested Sets

Описание

Каждому элементу сопоставляются свойства: левый и правый индекс, на основе которых будет производиться выборка дочерних элементов. Также, но необязательно, элемент может дополняться свойством уровень для указания желаемого уровня вложенности выбираемого элемента относительно корня или родительского элемента.

Запрос получения дочерних элементов строится на том факте, что для любого дочернего элемента выполняются условия:

левый индекс больше левого индекса родительского элемента;

правый индекс меньше правого индекса родительского элемента.

При создании и обновлении дерева левые и правые индексы элементов дерева, при его обходе в глубину, заполняются по определённым правилам.

Преимущества

Возможность получения дочерних элементов любых уровней вложенности с помощью простого одиночного запроса.

Недостатки

При использовании целочисленных типов для левого и правого индекса и уровня необходимо пересчитывать индексы всех связанных элементов в следующих случаях:

при вставке элементов;

при удалении элементов;

при изменении родительского элемента.

Пример

Бустинг на деревьях. Ансамбли, бэггинг и бустинг

Когда мы пытаемся предсказать целевую переменную с помощью любого алгоритма машинного обучения , главные причины отличий реальной и предсказанной переменной — это noise, variance и bias. Ансамбль помогает уменьшить эти факторы (за исключением noise — это неуменьшаемая величина).

Ансамбль

Ансамбль — это набор предсказателей, которые вместе дают ответ (например, среднее по всем). Причина почему мы используем ансамбли — несколько предсказателей, которые пытаюсь получить одну и ту же переменную дадут более точный результат, нежели одиночный предсказатель. Техники ансамблирования впоследствии классифицируются в Бэггинг и Бустинг.

Бэггинг

Бэггинг — простая техника, в которой мы строим независимые модели и комбинируем их, используя некоторую модель усреднения (например, взвешенное среднее, голосование большинства или нормальное среднее).

Обычно берут случайную подвыборку данных для каждой модели, так все модели немного отличаются друг от друга. Выборка строится по модели выбора с возвращением. Из-за того что данная техника использует множество некореллириющих моделей для построения итоговой модели, это уменьшает variance. Примером бэггинга служит модель случайного леса (Random Forest, RF)

Бустинг

Бустинг — это техника построения ансамблей, в которой предсказатели построены не независимо, а последовательно

Это техника использует идею о том, что следующая модель будет учится на ошибках предыдущей. Они имеют неравную вероятность появления в последующих моделях, и чаще появятся те, что дают наибольшую ошибку. Предсказатели могут быть выбраны из широкого ассортимента моделей, например, деревья решений , регрессия , классификаторы и т.д. Из-за того, что предсказатели обучаются на ошибках, совершенных предыдущими, требуется меньше времени для того, чтобы добраться до реального ответа. Но мы должны выбирать критерий остановки с осторожностью, иначе это может привести к переобучению. Градиентный бустинг — это пример бустинга.

Дерево (структура данных). Дерево, как структура данных

Какую выгоду можно извлечь из такой структуры данных, как дерево? В этой статье мы расскажем о данных в виде дерева, рассмотрим основные определения, которые следует знать, а также узнаем, как и зачем используется дерево в программировании . Спойлер: бинарные деревья часто применяют для поиска информации в базах данных, для сортировки данных, для проведения вычислений, для кодирования и в других случаях. Но давайте обо всем по порядку.

Основные термины

Дерево — это, по сути, один из частных случаев графа. Древовидная модель может быть весьма эффективна в случае представления динамических данных, особенно тогда, когда у разработчика стоит цель быстрого поиска информации, в тех же базах данных, к примеру. Еще древом называют структуру данных, которая представляет собой совокупность элементов, а также отношений между этими элементами, что вместе образует иерархическую древовидную структуру .

Каждый элемент — это вершина или узел дерева. Узлы, соединенные направленными дугами, называются ветвями . Начальный узел — это корень дерева (корневой узел). Листья — это узлы, в которые входит 1 ветвь, причем не выходит ни одной.

Общую терминологию можно посмотреть на левой и правой части картинки ниже:

Какие свойства есть у каждого древа:

— существует узел, в который не входит ни одна ветвь;

— в каждый узел, кроме корневого узла, входит 1 ветвь.

На практике деревья нередко применяют, изображая различные иерархии. Очень популярны, к примеру, генеалогические древа — они хорошо известны. Все узлы с ветвями, исходящими из единой общей вершины, являются потомками, а сама вершина называется предком (родительским узлом). Корневой узел не имеет предков, а листья не имеют потомков.

Также у дерева есть высота (глубина) . Она определяется числом уровней, на которых располагаются узлы дерева. Глубина пустого древа равняется нулю, а если  речь идет о дереве из одного корня, тогда единице. В данном случае на нулевом уровне может быть лишь одна вершина – корень, на 1-м – потомки корня, на 2-м – потомки потомков корня и т. д.

Ниже изображен графический вывод древа с 4-мя уровнями (дерево имеет глубину, равную четырем):

Следующий термин, который стоит рассмотреть, — это поддерево . Поддеревом называют часть древообразной структуры, которую можно представить в виде отдельного дерева.

Идем дальше. Древо может быть упорядоченным — в данном случае ветви, которые исходят из каждого узла, упорядочены по некоторому критерию.

Степень вершины в древе — это число ветвей (дуг), выходящих из этой вершины. Степень равняется максимальной степени вершины, которая входит в дерево. В этом случае листьями будут узлы, имеющие нулевую степень. По величине степени деревья бывают:

— двоичные (степень не больше двух);

— сильноветвящиеся (степень больше двух).

Деревья — это рекурсивные структуры , ведь каждое поддерево тоже является деревом. Каждый элемент такой рекурсивной структуры является или пустой структурой, или компонентом, с которым связано конечное количество поддеревьев.

Когда мы говорим о рекурсивных структурах, то действия с ними удобнее описывать посредством рекурсивных алгоритмов.

Обход древа

Чтобы выполнить конкретную операцию над всеми вершинами, надо все эти узлы просмотреть. Данную задачу называют обходом дерева . То есть обход представляет собой упорядоченную последовательность узлов, в которой каждый узел встречается лишь один раз.

В процессе обхода все узлы должны посещаться в некотором, заранее определенном порядке. Есть ряд способов обхода, вот три основные:

— прямой (префиксный, preorder);

— симметричный (инфиксный, inorder);

— обратный (постфиксный, postorder).

Существует много древовидных структур данных: двоичные (бинарные), красно-черные, В-деревья, матричные, смешанные и пр. Поговорим о бинарных.

Бинарные (двоичные) деревья

Бинарные имеют степень не более двух. То есть двоичным древом можно назвать динамическую структуру данных, где каждый узел имеет не большое 2-х потомков. В результате двоичное дерево состоит из элементов, где каждый из элементов содержит информационное поле, а также не больше 2-х ссылок на различные поддеревья. На каждый элемент древа есть только одна ссылка.

У бинарного древа каждый текущий узел — это структура, которая состоит из 4-х видов полей. Какие это поля:

— информационное (ключ вершины);

— служебное (включена вспомогательная информация, однако таких полей может быть несколько, а может и не быть вовсе);

— указатель на правое поддерево;

— указатель на левое поддерево.

Самый удобный вид бинарного древа — бинарное дерево поиска.

Что значит древо в контексте программирования?

Мы можем долго рассуждать о математическом определении древа, но это вряд ли поможет понять, какие именно выгоды можно извлечь из древовидной структуры данных. Тут важно отметить, что древо является способом организации данных в форме иерархической структуры .

Какие базы данных бывают. Реляционные базы данных (MySQL, PostgreSQL, Oracle DB)

На рисунке 1 я попыталась изобразить графически реляционную базу данных. Мы видим таблицы, из которых состоит база, и также видим, какие столбцы содержит каждая из таблиц.

Как я отметила выше, второй важной характеристикой реляционных баз данных является то, что между таблицами существуют отношения. Отношения между таблицами определяются с помощью primary key и foreign key.

Primary key  – это столбец (или группа столбцов) таблицы, который содержит уникальные значения для каждой строки. На примере выше primary key каждой таблицы я выделила зеленым цветом. То есть, например, в таблице с заказами каждая строка будет описывать отдельный заказ. Не будет 2 строк, которые описывают один и тот же заказ, потому ID заказа будет разный для каждой строки.

Foreign key  – это столбец в таблице, который содержит primary key другой таблицы. На рисунке foreign key отмечены желтым. То есть, таблица с заказами содержит ID клиента, который является primary key в таблице с клиентами, но в таблице с заказами он будет foreign key.

Primary key и foreign key помогают не только связывать между собой таблицы реляционной базы данных отношениями. Они еще помогают следить за целостностью и правильностью данных в базе. Например, если мы ошибемся в ID клиента, добавляя новый заказ в таблицу с заказами, то база выдаст ошибку, так как не найдет соответствующий ID клиента в таблице с клиентами.

Для взаимодействия с реляционными базами данных чаще всего используется  SQL  (Structured QueryLanguage). Это специальный язык программирования, на котором пишутся запросы к реляционной базе. SQL-запросами можно создавать и удалять таблицы в реляционной базе, изменять данные в существующих таблицах и доставать из таблиц необходимую информацию.

Как я уже говорила выше, реляционные базы данных удобно использовать в аналитике, так как информация в них структурирована и распределена по смыслу, что, конечно, мечта любого аналитика. Однако, аналитики часто пишут сложные и не очень эффективные SQL-запросы, потому важно придумывать способы ускорения обработки запросов к реляционной базе.

Одним из наиболее популярных методов ускорения работы запросов к реляционным базам данных является  индексирование таблиц . Индекс – это определенный столбец в таблице, по которому осуществляется поиск. 

Приведу пример работы индекса. Например, мы хотим найти все заказы клиента 007 из ресторана 1. Тогда, если у нас в таблице с заказами нет индекса, то мы будем перебирать все заказы пока не найдем нужные. Если же у нас есть индекс в таблице с заказами, то ситуация будет иной. Допустим, что индексом является столбец ID ресторана. Тогда наши данные в таблице с заказами будут сгруппированы по ID ресторана. И тогда при поиске заказов клиента 007 из ресторана 1, мы не будем перебирать всю таблицу с заказами, а найдем группу заказов из ресторана 1 и будем искать необходимые данные внутри этой группы.

Из примера выше с индексом выше понятно, что индексом удобно выбирать такой столбец, в разрезе которого часто ищутся данные.

Также, одним из важных свойств реляционных баз данных является  соответствие требованиям ACID . Я не буду углубляться в детали этих требований, только отмечу, что эти требования гарантируют целостность и корректность данных, несмотря на ошибки, системные сбои, перебои в питании, изменение данных несколькими пользователями одновременно и прочие необычные ситуации.

Выглядит так, что реляционная база данных идеальная база, и непонятно, почему бы постоянно ее не использовать. Однако, у реляционной базы данных есть и недостатки, и потому данный тип не всегда подходит для нужд бизнеса. Например, реляционная база данных не подходит для данных без четкой структуры, потому что мы не сможем разложить эти данные в отдельные таблицы по смыслу. А данных без четкой структуры гораздо больше, чем данных с четкой структурой.

Дерево программирование. Бинарное дерево —, что это? B-деревья

Статья расскажет о том, что такое бинарные деревья . Будут представлены способы их представления и основные термины. Отдельное внимание будет уделено B-дереву и его отличию от двоичных структур.

Деревом называют структуру данных, которая имеет древовидный вид, то есть характеризуется наличием набора связанных узлов. Бинарное дерево — это конечное множество элементов, связанных с двумя разными бинарными деревьями — правым и левым поддеревьями.

Способ представления:

На что следует обратить внимание: — А — корень дерева; — B — корень левого поддерева и предок D; — С — корень правого поддерева; — D — потомок родительского узла B; если D располагается на уровне i, то B – на уровне i-1.

Необходимо выделить следующие термины: — узел (вершина) — это каждый элемент бинарного дерева; — ветви — связи между узлами; — глубина (высота) — наибольший уровень какого-нибудь элемента; — лист (терминальный узел) — термин применяется, если элемент не имеет потомков; — внутренние узлы — узлы ветвления; — степень внутреннего узла — число его потомков (наибольшая степень всех существующих узлов — это степень всего бинарного дерева); — длина пути к x — количество ветвей, которые необходимо пройти от корня до текущего узла x. Длина пути самого корня равна нулю, а узел на уровне i обладает длиной пути, которая равна i.

Использование

На практике бинарные деревья применяются, когда в каждой точке какого-нибудь вычислительного процесса нужно принимать одно из 2-х возможных решений. Существует множество задач, решаемых таким способом. Одна из них — выполнение операции, условно говоря, X с каждым элементом дерева. X рассматривается в качестве параметра обобщенной задачи посещения всех вершин либо задачи обхода дерева. Если рассмотреть такую задачу в качестве единого последовательного процесса, то можно сказать, что отдельные вершины посещаются в определенном порядке, то есть могут считаться линейно расположенными.

Способы обхода

Предположим, что имеется дерево (не пустое), в котором A является корнем, а B и C — левым и правым поддеревьями.

Есть 3 способа обхода: 1. Обход в прямом порядке — сверху вниз: A, B, C — префиксная форма. 2. Обход слева направо (симметричный порядок): B, A, C — инфиксная форма. 3. Обход снизу вверх (обратный порядок): B, C, A — постфиксная форма.

Реализация

На практике вершину древа можно описать в качестве структуры:

Тогда обход в префиксной форме будет выглядеть следующим образом:

Теперь инфиксная форма:

И постфиксная:

Бинарное дерево поиска

Оно представляет собой двоичное (бинарное) дерево, для которого справедлив ряд дополнительных условий. Эти условия называют свойствами:

Данные в каждой вершине должны обладать ключами, где определена операция сравнения “

Обычно информация, которая представляет каждую вершину, — это запись, а не единственное поле данных.

Чтобы составить бинарное дерево поиска, пригодится функция добавления узла:

Удаляем поддерево

B-дерево. Поиск по B-дереву

В бинарном дереве поиска каждый узел содержит лишь одно значение (ключ) и не более 2-х потомков. Но существует особый вид древа поиска, называемый B-дерево (Би-дерево). Здесь узел содержит больше одного значения и больше 2-х потомков. Также его называют сбалансированным по высоте деревом поиска порядка m (Height Balanced m-way Search Tree).

B-дерево представляет собой сбалансированное дерево поиска, где каждый узел содержит много ключей и имеет больше 2-х потомков.

Возможные операции: 1. Поиск. 2. Вставка (вставляем новый элемент). 3. Удаление.

Каждое B-дерево имеет порядок. Для примера рассмотрим B-дерево порядка m. Оно будет обладать рядом следующих характеристик:

Ниже можно посмотреть на B-дерево четвертого порядка, содержащее максимум три значения ключа и максимум четыре потомка для каждой вершины.

Поиск аналогичен поиску по двоичному дереву. Следует вспомнить, что в двоичном древе поиск начинается с корня, причем каждый раз принимается 2-стороннее решение (пойти по правому поддереву либо по левому). В В-дереве поиск тоже начинается с корневого узла, но с той лишь разницей, что на каждом шаге принимается не 2-стороннее, а n-стороннее решение, причем n для дерева в данном случае представляет общее число потомков рассматриваемого узла. Сложность поиска такого дерева — O(log n).

Алгоритм следующий:

Также существует такое понятие, как вставка в B-дерево.

Дерево информатика. 1 Что такое деревья (в программировании)?

Математическое определение дерева — «без петель и циклов» вряд-ли пояснит рядовому человеку какие выгоды можно извлечь из такой структуры данных.

В некоторых книгах, посвященным разработке алгоритмов, деревья определяются рекурсивно . Дерево является либо пустым, либо состоит из узла ( корня ), являющегося родительским узлом для некоторого количества деревьев (это количество определяет арность дерева ) .

Рабочее определение (в рамках этой статьи): дерево — это способ организации данных в виде иерархической структуры .

Когда применяются древовидные структуры:

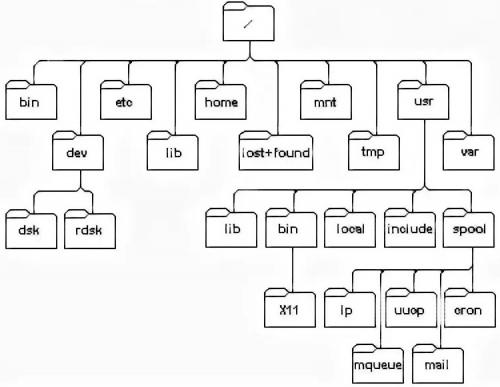
1. иногда такая иерархия существует в предметной области вашей программы, например, она должна обрабатывать гениалогическое дерево или работать со структурой каталогов на жестком диске. В таких случаях инода имеет смысл сохранить между объектами вашей программы существующие отношения иерархии:
   

   

   Дерево каталогов операционной системы UNIX

2. в других случаях между объектами, которые обрабатывает ваша программа отношения иерархии явно не заданы, однако, их можно задать и это сделает обработку данных в программе более удобной . Например, при разработке парсеров или трансляторов полезным может оказаться дерево синтаксического разбора ( синтаксическое дерево ) , хотя в выражениях типа «1+7*3» иерархия операций не так очевидна ;
3. не секрет, что поиск объектов наиболее эффективен если они упорядочены. В частности, поиск значения в неупорядоченном наборе из 1000 элементов в худшем случае потребует 1000 операций, а в упорядоченном — можно обойтись всего 10.
   

   Двоичный поиск выполняется над отсортированным массивом. На каждом шаге искомый элемент сравнивается со значением, находящимся посередине массива. В зависимости от результатов сравнения — либо левая, либо правая части могут быть «отброшены».

   Иерархия — способ упорядочивания объектов , соответственно применять ее можно для ускорения поиска . Именно этому посвящена остальная часть статьи.