Все Что нужно знать о древовидных структурах данных. Основные определения
- Все Что нужно знать о древовидных структурах данных. Основные определения
- Древовидная структура. Описание структуры
- Дерево структура. Основные термины
- Дерево в информатике пример. 1 Что такое деревья (в программировании)?
- Структура данных дерево C#. Простой шаблон класса дерева на C#
- Все структуры данных. Структуры данных. Типы структур данных
- Структуры данных. 10 типов структур данных, которые нужно знать
- Бинарное дерево структура данных. Двоичное дерево
Все Что нужно знать о древовидных структурах данных. Основные определения
Структуры данных типа “дерево” исключительно широко используются в программной индустрии. В отличие от списковых структур деревья относятся к нелинейным структурам. Любое дерево состоит из элементов – узлов или вершин, которые по определенным правилам связаны друг с другом рёбрами. В списковых структурах за текущей вершиной (если она не последняя) всегда следует только одна вершина, тогда как в древовидных структурах таких вершин может быть несколько . Математически дерево рассматривается как частный случай графа, в котором отсутствуют замкнутые пути (циклы).
Дерево является типичным примером рекурсивно определённой структуры данных, поскольку оно определяется в терминах самого себя.
Рекурсивное определение дерева с базовым типом Т – это:
либо пустое дерево (не содержащее ни одного узла)
либо некоторая вершина типа Т с конечным числом связанных с ней отдельных деревьев с базовым типом Т, называемых поддеревьями
Отсюда видно, что в любом непустом дереве есть одна особая вершина – корень дерева, которая как бы определяет “начало” всего дерева. С другой стороны, существуют и вершины другого типа, не имеющие связанных с ними поддеревьев. Такие вершины называют терминальными или листьями.
Классификацию деревьев можно провести по разным признакам.
1. По числу возможных потомков у вершин различают двоичные (бинарные ) или недвоичные (сильноветвящиеся) деревья.
Двоичное дерево: каждая вершина может иметь не более двух потомков.
Недвоичное дерево: вершины могут иметь любое число потомков.
2. Если в дереве важен порядок следования потомков, то такие деревья называют упорядоченными. Для них вводится понятие левый и правый потомок (для двоичных деревьев) или более левый/правый (для недвоичных деревьев). В этом смысле два следующих простейших упорядоченных дерева с одинаковыми элементами считаются разными :
При использовании деревьев часто встречаются такие понятия как путь между начальной и конечной вершиной (последовательность проходимых ребер или вершин), высота дерева (наиболее длинный путь от корневой вершины к терминальным).
При рассмотрении дерева как структуры данных необходимо четко понимать следующие два момента:
Все вершины дерева, рассматриваемые как переменные языка программирования, должны быть одного и того же типа, более того – записями с некоторым информационным наполнением и необходимым количеством связующих полей
В силу естественной логической разветвленности деревьев (в этом весь их смысл!) и отсутствия единого правила выстраивания вершин в порядке друг за другом, их логическая организация не совпадает с физическим размещением вершин дерева в памяти.
Древовидная структура. Описание структуры
Как правило, такая структура данных предполагает хранение информации о смежных вершинах нашего дерева. Давайте рассмотрим простейший граф с темя вершинами (1,2,3): Рис. 1. Граф с тремя вершинами Как видим каждый элемент данного графа хранит информацию о связи с другими элементами, т.е.:1 - 2,3 2 - 1,3 3 - 1,2
Фактически, для построения дерева такой граф избыточен, т.к. для привычной ветвистой структуры нам нужно хранить только связь «родитель-наследник», т.е.:2-1 3-1
Тогда мы получим дерево с одним корневым элементом (1) и двумя ветками (2,3): Рис. 2. Граф дерева В принципе, тот и другой графы можно, при желании, отобразить в базе данных с помощью списка смежных вершин, но, поскольку нас интересуют именно деревья, остановимся на них.Итак, чтобы хранить в базе данных иерархическую структуру методом списка смежных вершин (Adjacency List), нам необходимо хранить информацию о связях «наследник-родитель» в таблицах с данными. Давайте рассмотрим реальный пример дерева: Рис. 3. Древовидная структура методом смежных вершин На рисунке квадратами обозначены узлы деревьев. У каждого узла есть имя (верхний прямоугольник внутри квадрата), идентификатор (левый нижний квадрат) и ссылка на идентификатор родителя (правый нижний квадрат). Как видно из Рис. 3, каждый наследник в такой структуре ссылается на своего предка. В терминах БД мы можем это отобразить следующим образом в виде таблицы: Рис. 4. Таблица данных дерева, построенная методом списка смежных вершин Или же в виде SQL:CREATE TABLE al_tree ( `id` BIGINT NOT NULL AUTO_INCREMENT PRIMARY KEY, `parent_id` BIGINT NULL, `name` VARCHAR(50) NOT NULL ) TYPE=InnoDB DEFAULT CHARSET=utf8; CREATE INDEX fk_tree_tree ON al_tree (parent_id); ALTER TABLE al_tree ADD CONSTRAINT fk_tree_tree FOREIGN KEY (parent_id) REFERENCES al_tree (id) ON UPDATE CASCADE ON DELETE CASCADE; INSERT INTO al_tree VALUES (1, NULL, 'FOOD'), (2, 1, 'VEGETABLE'), (3, 2, 'POTATO'), (4, 2, 'TOMATO'), (5, 1, 'FRUIT'), (6, 5, 'APPLE'), (7, 5, 'BANANA');
Следует сразу отметить, что такой алгоритм хранения деревьев обладает определенными как достоинствами, так и недостатками. В первую очередь, он не совсем удобен для чтения — и это его основной недостаток.Проблемы с чтением из БД менее заметны, если вычитывать все дерево целиком. Это достаточно простой запрос:+----+-----------+-----------+ | id | parent_id | name | +----+-----------+-----------+ | 1 | NULL | FOOD | | 2 | 1 | VEGETABLE | | 3 | 2 | POTATO | | 4 | 2 | TOMATO | | 5 | 1 | FRUIT | | 6 | 5 | APPLE | | 7 | 5 | BANANA | +----+-----------+-----------+
Однако в дальнейшем такая выборка подразумевает достаточно емкую программную пост-обработку данных. Сначала нужно рекурсивно перестроить данные с учетом связей «предок-наследник» и лишь потом их можно будет использовать для вывода куда-либо.Другой вариант чтения дерева целиком:SELECT t1.name AS lvl1, t2.name as lvl2, t3.name as lvl3 FROM al_tree AS t1 LEFT JOIN al_tree AS t2 ON t2.parent_id = t1.id LEFT JOIN al_tree AS t3 ON t3.parent_id = t2.id LEFT JOIN al_tree AS t4 ON t4.parent_id = t3.id WHERE t1.id = 1;
Результат в данном случае будет такой:+------+-----------+--------+ | lvl1 | lvl2 | lvl3 | +------+-----------+--------+ | FOOD | VEGETABLE | POTATO | | FOOD | VEGETABLE | TOMATO | | FOOD | FRUIT | APPLE | | FOOD | FRUIT | BANANA | +------+-----------+--------+
Хотя данные в таком виде уже более приспособлены сразу для вывода, но, как видите, главный недостаток такого подхода — необходимо достоверно знать количество уровней вложенности в вашей иерархии, кроме того, чем больше иерархия, тем больше JOIN'ов — тем ниже производительность.Тем не менее, данный способ обладает и существенными достоинствами — в дерево легко вносить изменения, менять местами и удалять узлы.Вывод — данный алгоритм хорошо применим, если вы оперируете с небольшими древовидными структурами, которые часто поддаются изменениям.С другой стороны, этот алгоритм также довольно уверенно себя чувствует и с большими деревьями, если считывать их порциями вида «знаю родителя — прочитать всех наследников». Хороший пример такого случая — динамически подгружаемые деревья. В этом случае алгоритм практически оптимизирован для такого поведения.Однако он плохо применим, когда нужно вычитывать какие-либо иные куски дерева, находить пути, предыдущие и следующие узлы при обходе и вычитывать ветки дерева целиком (на всю глубину).Дерево структура. Основные термины
Дерево — это, по сути, один из частных случаев графа. Древовидная модель может быть весьма эффективна в случае представления динамических данных, особенно тогда, когда у разработчика стоит цель быстрого поиска информации, в тех же базах данных, к примеру. Еще древом называют структуру данных, которая представляет собой совокупность элементов, а также отношений между этими элементами, что вместе образует иерархическую древовидную структуру .
Каждый элемент — это вершина или узел дерева. Узлы, соединенные направленными дугами, называются ветвями . Начальный узел — это корень дерева (корневой узел). Листья — это узлы, в которые входит 1 ветвь, причем не выходит ни одной.
Общую терминологию можно посмотреть на левой и правой части картинки ниже:
Какие свойства есть у каждого древа:
— существует узел, в который не входит ни одна ветвь;
— в каждый узел, кроме корневого узла, входит 1 ветвь.
На практике деревья нередко применяют, изображая различные иерархии. Очень популярны, к примеру, генеалогические древа — они хорошо известны. Все узлы с ветвями, исходящими из единой общей вершины, являются потомками, а сама вершина называется предком (родительским узлом). Корневой узел не имеет предков, а листья не имеют потомков.
Также у дерева есть высота (глубина) . Она определяется числом уровней, на которых располагаются узлы дерева. Глубина пустого древа равняется нулю, а если речь идет о дереве из одного корня, тогда единице. В данном случае на нулевом уровне может быть лишь одна вершина – корень, на 1-м – потомки корня, на 2-м – потомки потомков корня и т. д.
Ниже изображен графический вывод древа с 4-мя уровнями (дерево имеет глубину, равную четырем):
Следующий термин, который стоит рассмотреть, — это поддерево . Поддеревом называют часть древообразной структуры, которую можно представить в виде отдельного дерева.
Идем дальше. Древо может быть упорядоченным — в данном случае ветви, которые исходят из каждого узла, упорядочены по некоторому критерию.
Степень вершины в древе — это число ветвей (дуг), выходящих из этой вершины. Степень равняется максимальной степени вершины, которая входит в дерево. В этом случае листьями будут узлы, имеющие нулевую степень. По величине степени деревья бывают:
— двоичные (степень не больше двух);
— сильноветвящиеся (степень больше двух).
Деревья — это рекурсивные структуры , ведь каждое поддерево тоже является деревом. Каждый элемент такой рекурсивной структуры является или пустой структурой, или компонентом, с которым связано конечное количество поддеревьев.
Когда мы говорим о рекурсивных структурах, то действия с ними удобнее описывать посредством рекурсивных алгоритмов.
Дерево в информатике пример. 1 Что такое деревья (в программировании)?
Математическое определение дерева — «без петель и циклов» вряд-ли пояснит рядовому человеку какие выгоды можно извлечь из такой структуры данных.
В некоторых книгах, посвященным разработке алгоритмов, деревья определяются рекурсивно . Дерево является либо пустым, либо состоит из узла ( корня ), являющегося родительским узлом для некоторого количества деревьев (это количество определяет арность дерева ) .
Рабочее определение (в рамках этой статьи): дерево — это способ организации данных в виде иерархической структуры .
Когда применяются древовидные структуры:
- иногда такая иерархия существует в предметной области вашей программы, например, она должна обрабатывать гениалогическое дерево или работать со структурой каталогов на жестком диске. В таких случаях инода имеет смысл сохранить между объектами вашей программы существующие отношения иерархии:

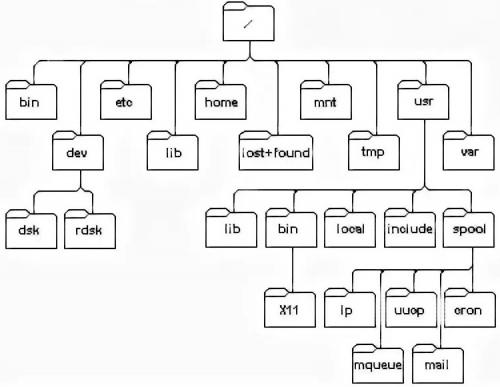
Дерево каталогов операционной системы UNIX
- в других случаях между объектами, которые обрабатывает ваша программа отношения иерархии явно не заданы, однако, их можно задать и это сделает обработку данных в программе более удобной . Например, при разработке парсеров или трансляторов полезным может оказаться дерево синтаксического разбора ( синтаксическое дерево ) , хотя в выражениях типа «1+7*3» иерархия операций не так очевидна ;
- не секрет, что поиск объектов наиболее эффективен если они упорядочены. В частности, поиск значения в неупорядоченном наборе из 1000 элементов в худшем случае потребует 1000 операций, а в упорядоченном — можно обойтись всего 10.
Двоичный поиск выполняется над отсортированным массивом. На каждом шаге искомый элемент сравнивается со значением, находящимся посередине массива. В зависимости от результатов сравнения — либо левая, либо правая части могут быть «отброшены».
Иерархия — способ упорядочивания объектов , соответственно применять ее можно для ускорения поиска . Именно этому посвящена остальная часть статьи.
Структура данных дерево C#. Простой шаблон класса дерева на C#
Консольное приложение "решёток", показывающее, что при реализации "древовидного" шаблона средствами хоть STL , хоть встроенных в .NETSystem.Collections, "само дерево"-то и не нужно, достаточно реализации функциональности узлаTreeNode.
Эту реализацию, собственно, и показывает файлTreeNode.cs, аExampleOfMain.csсодержит примеры формирования дерева, обхода с выводом в консоль (отступы соблюдаются), поиска и удаления узла.
Ниже приводятся исходники файлов и проект, проверенный в актуальной сборке Visual Studio 2019.
Все структуры данных. Структуры данных. Типы структур данных
265
Структура данных — это «контейнер», который используется для хранения и организации данных по определенным правилам. Это способ упорядочивания данных на компьютере таким образом, чтобы к ним можно было эффективно получать доступ и вносить изменения.
В зависимости от требований и проекта важно выбрать оптимальную структуру данных. Например, если вы хотите хранить данные последовательно в памяти, то можно воспользоваться Массивом.
Примечание: Структура данных и типы данных немного различаются. Структура данных — это набор типов данных, упорядоченных в определенном порядке.
Типы структур данных
В основном, структуры данных делятся на два типа:
Линейные структуры данных.
Нелинейные структуры данных.
Рассмотрим их детально.
Линейные структуры данных
В линейных структурах данных элементы располагаются последовательно друг за другом. Поскольку элементы упорядочены в определенном порядке, данную структуру относительно легко создать и поддерживать. Однако с увеличением сложности программы линейные структуры данных уже могут быть не лучшим вариантом из-за операционных сложностей.
Рассмотрим наиболее популярные линейные структуры данных.
Структура данных Массив
В массиве элементы в памяти располагаются в непрерывной последовательности. Все элементы массива имеют одинаковый тип. Тип элементов, которые можно хранить в виде массивов, определяется языком программирования.
Структура данных Стек
В стеке элементы хранятся по (сокр. от англ.). Это означает, что последний элемент, добавленный в стек, удаляется первым.
Структура данных Очередь
В отличие от стека, очередь работает по принципу FIFO (сокр. от англ.), где первый элемент, помещенный в очередь, первым и удаляется.
Структура данных Связный список
В связном списке данные связаны через серию узлов. Каждый узел содержит элементы данных и адрес следующего узла. Посредством адреса и осуществляется «связывание».
Связный список
Нелинейные структуры данных
В отличие от линейных структур данных, элементы в нелинейных структурах данных не расположены в какой-либо последовательности. Вместо этого они организованы иерархически, где один элемент связан с другим или сразу несколькими другими элементами.
Нелинейные структуры данных делятся на графовые и древовидные структуры данных.
Структура данных Граф
В графе каждый узел называется вершиной, а каждая вершина соединена с другими вершинами через ребра.
Пример структуры данных Граф
Древовидные структуры данных
Подобно графу, дерево также представляет собой набор вершин и ребер. Однако в древовидной структуре данных между двумя вершинами может быть только одно ребро.
Структуры данных. 10 типов структур данных, которые нужно знать
«Плохие программисты думают о коде. Хорошие программисты думают о структурах данных и их взаимосвязях», — Линус Торвальдс, создатель Linux.
Структуры данных играют важную роль в процессе разработки ПО, а еще по ним часто задают вопросы на собеседованиях для разработчиков. Хорошая новость в том, что по сути они представляют собой всего лишь специальные форматы для организации и хранения данных.
Программа обучения: « Big Data: основы работы с большими массивами данных »
В этой статье я покажу вам 10 самых распространенных структур данных. Для каждой из них приведены видео и примеры их реализации на JavaScript. Чтобы вы смогли попрактиковаться, я также добавил несколько упражнений из бета-версии новой учебной программы freeCodeCamp.
Обратите внимание, что некоторые структуры данных включают временную сложность в нотации «большого О». Это относится не ко всем из них, так как иногда временная сложность зависит от реализации. Если вы хотите узнать больше о нотации «большого О», посмотрите это видео от Briana Marie .
Офлайн-курс: « Data Scientist »
В статье я привожу примеры реализации этих структур данных на JavaScript: они также пригодятся, если вы используете низкоуровневый язык вроде С. В многие высокоуровневые языки, включая JavaScript, уже встроены реализации большинства структур данных, о которых пойдет речь. Тем не менее, такие знания станут серьезным преимуществом при поиске работы и пригодятся при написании высокопроизводительного кода.
Связные списки
Связный список — одна из базовых структур данных. Ее часто сравнивают с массивом, так как многие другие структуры можно реализовать с помощью либо массива, либо связного списка. У этих двух типов есть преимущества и недостатки.
Так устроен связный список
Связный список состоит из группы узлов, которые вместе образуют последовательность. Каждый узел содержит две вещи: фактические данные, которые в нем хранятся (это могут быть данные любого типа) и указатель (или ссылку) на следующий узел в последовательности. Также существуют двусвязные списки: в них у каждого узла есть указатель и на следующий, и на предыдущий элемент в списке.
Основные операции в связном списке включают добавление, удаление и поиск элемента в списке.
Пример реализации на JavaScript
Временная сложность связного списка
Упражнения от freeCodeCamp
- Work with Nodes in a Linked List
- Create a Linked List Class
- Remove Elements from a Linked List
- Search within a Linked List
- Add Elements at a Specific Index in a Linked List
- Create a Doubly Linked List
- Reverse a Doubly Linked List
Стеки
Стек — это базовая структура данных, которая позволяет добавлять или удалять элементы только в её начале. Она похожа на стопку книг: если вы хотите взглянуть на книгу в середине стека, сперва придется убрать лежащие сверху.
Стек организован по принципу LIFO (Last In First Out, «последним пришёл — первым вышел») . Это значит, что последний элемент, который вы добавили в стек, первым выйдет из него.
Так устроен стек
В стеках можно выполнять три операции: добавление элемента (push), удаление элемента (pop) и отображение содержимого стека (pip).
Пример реализации на JavaScript
Временная сложность стека
Упражнения от freeCodeCamp
- Learn how a Stack Works
- Create a Stack Class
Очереди
Эту структуру можно представить как очередь в продуктовом магазине. Первым обслуживают того, кто пришёл в самом начале — всё как в жизни.
Так устроена очередь
Очередь устроена по принципу FIFO (First In First Out, «первый пришёл — первый вышел»). Это значит, что удалить элемент можно только после того, как были убраны все ранее добавленные элементы.
Очередь позволяет выполнять две основных операции: добавлять элементы в конец очереди (enqueue) и удалять первый элемент (dequeue).
Бинарное дерево структура данных. Двоичное дерево
Двои́чное де́рево — иерархическая структура данных , в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками. Двоичное дерево является упорядоченным ориентированным деревом .
Для практических целей обычно используют два подвида двоичных деревьев — двоичное дерево поиска и двоичная куча .
Существует следующее рекурсивное определение двоичного дерева (см. БНФ ):
::= ( ) | null .
То есть двоичное дерево либо является пустым, либо состоит из данных и двух поддеревьев (каждое из которых может быть пустым). Очевидным, но важным для понимания фактом является то, что каждое поддерево в свою очередь тоже является деревом. Если у некоторого узла оба поддерева пустые, то он называется листовым узлом (листовой вершиной) или конечным (терминальным) узлом.
Например, показанное справа на рис. 1 дерево согласно этой грамматике можно было бы записать так:
(m (e (c (a null null) null ) (g null (k null null) ) ) (s (p (o null null) (s null null) ) (y null null) ) ) | Рис. 1. Двоичное дерево поиска, в котором ключами являются латинские символы упорядоченные по алфавиту. |