2-3-4-дерево и красно-черное дерево. Основное назначение красно-черного дерева по сравнению с другими деревьями:

2-3-4-дерево и красно-черное дерево. Основное назначение красно-черного дерева по сравнению с другими деревьями:

1. Основная цель - поиск
2. AVL и красно-черное дерево являются вариантами двоичного дерева поиска.
3. Дерево AVL строго сбалансировано, а красно-черное дерево сбалансировано черным. Но поддержание баланса требует дополнительных операций, что также увеличивает временную сложность структуры данных, поэтому красно-черное дерево можно рассматривать как компромисс между бинарным деревом поиска и деревом AVL, вы можете попытаться сохранить баланс дерева без Слишком много времени, чтобы сохранить природу структуры данных.
4. AVL подходит для красных и черных деревьев Внутренняя память Использовать
Статистическая производительность красно-черных деревьев лучше, чем AVL, но экстремальная производительность немного хуже.
5. Дерево AVL подходит для Вставьте и удалите меньше, но найдите больше 。
при использовании для поиска, Когда есть много вставок и удалений Далее мы используем красные и черные деревья
Windows использует дерево AVL для управления адресным пространством процесса
6. Подгонка B-дерева Внешнее хранилище Использовать
B дерево, B + дерево: Многолучевое дерево поиска Обычно используется для индексации в базе данных, потому что они имеют больше ветвей и меньше слоев. Поскольку дисковый ввод-вывод занимает очень много времени и большой объем данных хранится на диске, мы должны эффективно сократить количество дисковых операций ввода-вывода, чтобы избежать частых обращений к диску. Проблема с AVL и красно-черными деревьями заключается в том, что высота слоя дерева слишком велика. При запросе диска сначала нужно перейти в соответствующий сектор и найти местоположение узла в следующем слое, а затем перейти к следующему слою, найти узел, Продолжайте поиск. Для 1024 данных двоичное дерево требует 10 слоев, и в запросе слишком много секторов.
B + дерево - это дерево вариантов дерева B. Узлы с n поддеревьями содержат n ключевых слов. Каждое ключевое слово не сохраняет данные, оно используется только для индексации, а данные хранятся в листьях. узел. Он был рожден для файловой системы.
Дерево B + для чтения и записи дешевле, чем диск дерева B: поскольку неконечные узлы дерева B + хранят только значения ключей, один узел занимает меньше места, а индексный блок может хранить больше узлов, от Диск требует меньше индексных блоков для чтения индекса, поэтому количество операций ввода-вывода во время поиска по индексу меньше, чем у индекса B-Tree, и эффективность выше. Более того, записи, хранящиеся в конечных узлах B + Tree, связаны в виде связанного списка, и поиск или обход диапазона более эффективен. Mysql InnoDB использует индекс B + Tree.
6. Три дерево, также известное как дерево поиска слов, обычно используется для управления строками, Это только одна копия одного и того же префикса для разных строк , Относительно непосредственное сохранение строк определенно экономит место, но это будет очень сложно, когда экономит большое количество строк Потребление памяти (Это память).
Сходными являются: дерево префиксов (дерево префиксов), дерево суффиксов (дерево суффиксов), дерево оснований (дерево Патрисии, дерево компактных префиксов), дерево критических битов (для решения проблемы потребления памяти) и Двойной массив три, упомянутый ранее.
Префиксное дерево : Быстрый поиск строк, сортировка строк, самый длинный общий префикс, суффикс отображения автоматического соответствия префикса.
Суффикс дерево : Найти число вхождений строки s1 в s2, вхождение строки s1 в s2, самую длинную общую часть строк s1, s2 и самую длинную строку палиндрома.

Красно-черное дерево применение. Введение в Red Black Tree

Прежде всего, красно-черное дерево - это двоичное дерево поиска, которое добавляет бит памяти к каждому узлу, чтобы представить цвет узла, который может быть КРАСНЫМ или ЧЕРНЫМ. Ограничивая цвет каждого узла на простом пути от корневого узла до конечного узла NIL (относится к пустому узлу или сигнальному индикатору ниже), красно-черное дерево гарантирует, что ни один путь не будет вдвое длиннее других путей. Это примерно сбалансировано. Чтобы

использовать

Красно-черные деревья, такие как деревья AVL, обеспечивают наилучшую возможную гарантию наихудшего случая для времени вставки, времени удаления и времени поиска. Временная сложность динамических операций, таких как поиск, вставка, удаление, максимум, минимум и т. Д., Составляет O (lgn). Обычно используются следующие:

• Установленная карта в STL (Standard Template Library) реализована на основе красно-черных деревьев.
• Красно-черные деревья также используются в TreeMap в Java.
• Реализация epoll в ядре использует красно-черное дерево для управления блоками событий.
• Планирование процессов Linux Полностью справедливый планировщик, с использованием блока управления процессом управления красно-черным деревом

Красно-черное дерево VS AVL Tree

Общие сбалансированные деревья включают красно-черные деревья и сбалансированные деревья AVL.Почему STL и Linux используют красно-черные деревья как реализацию сбалансированных деревьев? Вероятно, по следующим причинам:

С точки зрения деталей реализации, если вставка узла приводит к несбалансированности дерева, как для AVL-дерева, так и для красно-черного дерева требуется не более 2 операций вращения, то есть оба являются O (1); но удаление узла приводит к разбалансировке дерева. При балансировке, в худшем случае, AVL необходимо поддерживать баланс всех узлов на пути от удаленного узла к корню. Следовательно, порядок величины вращения - O (logN), в то время как RB-Tree требуется не более 3 оборотов. Требуется O (1) сложность

С точки зрения требований к балансу двух сбалансированных деревьев структура AVL более сбалансирована, чем структура RB-Tree. Вставка и удаление узлов с большей вероятностью вызовет дисбаланс дерева. Поэтому, когда необходимо вставить или удалить большой объем данных, требуется AVL. Частота ребалансировки будет выше. Следовательно, RB-Tree более эффективно в сценариях, когда необходимо вставить и удалить большое количество узлов. Естественно, поскольку AVL хорошо сбалансирован, поиск AVL более эффективен.

В целом статистическая производительность RB-дерева выше, чем у AVL.

Красно-черное дерево Python. Build the Forest in Python Series: AVL Tree vs Red-Black Tree

Being a good software engineer not only needs to know what tools (e.g., data structures and algorithms) are available but also understand how to choose the right tools. In addition, a good software engineer also requires the knowledge of how to measure if the tool we choose does work as we expect. This article is not going to build a new tree data structure like the previous articles. Instead, we will build a tool, a Python library called Metrics, that can monitor software behavior and performance, and then we can use the tool to prove our AVL tree and red-black tree work as they should be. Although we use the AVL tree and the red-black tree as an example, the idea we measure these trees can be applied to any software and real-world situation.

AVL tree and Red-Black Tree are often compared with each other because they both provide time complexity for their core operations: O(lg n), where n is the number of nodes (in the rest of the article, if not mention, n means the number of nodes). Many textbooks and articles have proven these two trees’ performance and complexity in theory. However, computer software (or computer science in general) is a practical subject. There are many ways to implement the same idea, algorithm, and data structure. Moreover, we also need to modify our implementation to fit our practical constraints, such as memory limitation, meaning the implementation does not strictly stick with the original definition. With this thought, the article tries to view these two trees in a more practical way — by measuring them and comparing them using the Metrics library we are going to build.

What do we measure?

The key of the AVL tree and the red-black tree to keep them balanced is rotation, so we will measure the number of rotations when insertion and deletion occur. In addition, we also want to monitor the change of tree height, so we know the trees are balanced all the time.

How to do that?

As we mentioned above, we will use the Metrics library to track our trees. If we want to measure our software’s behavior, we can inject some code into our software, and the piece of code keeps tracking the software’s behavior. Here, the Metrics library we will build is the piece of code that does the work.

Красно-черное дерево java. Red Black Tree

In this article, we will look at the red black treeand its different properties.Red black tree is an important data structure and provides a lot of benefits and advantages.

A red black tree is a self-balancingwhere each node has an extra bit containing the information about the color of the node (RED or BLACK). A red black tree is an extension of the binary search tree. This color information is used to ensure that the tree remains balanced during the insertion or deletion process.

A red black tree is not as strictly balanced as an AVL tree but is .

With this extra bit of information, our tree contains the following information:

• – Data being stored in the red black tree.
left– left child information. right– right child information. color– color information of the node if the node is red or black.

2. Red and Back Tree Properties

Red black tree is a binary search tree with few properties which help in the self balancing the binary tree.Here are the red back tree properties which should be satisfied if we want to call it and red and black tree.

1. The root node of the tree is always black.
2. Every node of the tree is red or black.
3. if a node is red, both children are black.
4. every path from root node to the leaf node has the same number of black nodes.

Here is a sample red black tree

Красно-черное дерево с++ код. Как реализовать красно-черное дерево в С++?

Нужна помощь с красно-черным деревом
Как свести эти части кода в одно целое, нужно чтобы после ввода каждого нового элемента, выводился максимальный элемент дерева и его цвет.
Вот код.

#include 
using namespace std;
 
struct node // структура для представления узлов дерева
{
 int key;
 unsigned char height;
 node* left;
 node* right;
 node(int k) { key = k; left = right = 0; height = 1; }
};
 
unsigned char height(node* p)
{
 return p ? p->height : 0;
}
 
int bfactor(node* p)
{
 return height(p->right) - height(p->left);
}
 
void fixheight(node* p)
{
 unsigned char hl = height(p->left);
 unsigned char hr = height(p->right);
 p->height = (hl>hr ? hl : hr) + 1;
}
 
node* rotateright(node* p) // правый поворот вокруг p
{
 node* q = p->left;
 p->left = q->right;
 q->right = p;
 fixheight(p);
 fixheight(q);
 return q;
}
 
node* rotateleft(node* q) // левый поворот вокруг q
{
 node* p = q->right;
 q->right = p->left;
 p->left = q;
 fixheight(q);
 fixheight(p);
 return p;
}
 
node* balance(node* p) // балансировка узла p
{
 fixheight(p);
 if (bfactor(p) == 2)
 {
 if (bfactor(p->right) right = rotateright(p->right);
 return rotateleft(p);
 }
 if (bfactor(p) == -2)
 {
 if (bfactor(p->left) > 0)
 p->left = rotateleft(p->left);
 return rotateright(p);
 }
 return p; // балансировка не нужна
}
 
node* insert(node* p, int k) // вставка ключа k в дерево с корнем p
{
 if (!p) return new node(k);
 if (kkey)
 p->left = insert(p->left, k);
 else
 p->right = insert(p->right, k);
 return balance(p);
}

Красно-черное дерево алгоритм. 2-3-дерево

Чтобы понять красно-чёрное дерево, нужно понять 2-3-дерево.

Забегая вперед, скажу, что 2-3-дерево — это, по сути, родитель нашего КЧД, поэтому важно начать именно с него. Поймем 2-3-дерево — поймём и КЧД.

2-3-дерево — абстрактный тип данных, напоминающий по структуре дерево. В нодах 2-3-дерева может быть одно или два значения и два или три потомка (от чего зависит количество значений и потомков ноды, узнаем ниже). Ноду с одним значением и двумя потомками будем называть 2-нода, ноду с двумя значениями и тремя потомками — 3-нода. Объяснение я начну с создания такого дерева: это наглядно и просто. Но некоторые уточнения всё же нужны:

1. Добавляя элемент, мы всегда спускаемся вниз по дереву.
2. Дерево отсортировано классически — меньшие значения находятся слева, бОльшие — справа.
3. 2-3-дерево — отсортированное, сбалансированное дерево.

Итак, начнём с первой ноды, это число 5. Тут всё просто — 5 становится корнем.

Добавим число 12. Его мы также добавляем в корень (помним, что нода может иметь два значения), но теперь нам нужно отсортировать нашу ноду (сортировать два элемента, ха), т.е. уложить их в порядке возрастания. В итоге получается нода 5-12.

Добавим следующее число. Пусть это будет 17. Давайте пока добавим наш элемент в единственную ноду и снова отсортируем ее. Получилась нода 5-12-17.

Внимательный читатель заметит тут подвох — выше я говорил о том, что наши ноды могут содержать не более двух элементов. Вот тут и происходит магия! Мы берём средний элемент нашей ноды и проталкиваем его наверх. Итог виден на картинке. Корнем стало число 12, левым сыном — число 5, правым — 17.

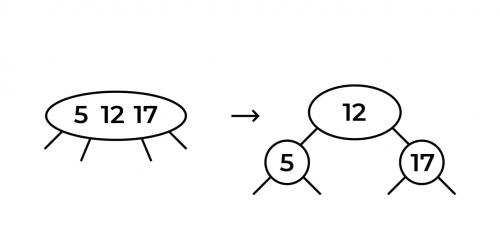
То, что мы сделали выше, можно назвать балансировкой 2-3-дерева. Правило в этой балансировке простое: если в ноде оказывается 3 значения, среднее мы проталкиваем наверх. Алгоритм действий зависит от трёх условий:

1. Нода является корнем. Тогда ничего не остаётся, как создать новую ноду с одним значением и сделать её новым корнем (как в нашем случае).
2. Родительская нода имеет одно значение. Тогда мы просто добавляем значение к родителю и завершаем балансировку (при этом у родителя появляется третий потомок).
3. Родительская нода имеет два значения. Тогда мы снова проталкиваем значение вверх, пока не придём к пункту 1 или 2.